Lors de l’élaboration d’une carte, l’une des étapes qui nous embêtent le plus c’est le moment où nous devons définir le système de projection. C’est un problème qui est survenu au moins une fois à toutes les personnes qui créent souvent des cartes.
Il nous arrive de nous demander quel système de projection choisir. Quel est le système qui est adapté à ma carte ? Quel impacte le choix du système aura sur la qualité de ma carte…
Si vous vous êtes au moins posé une de ces questions, alors cet article va vous intéressé.
Dans cet article, vous allez découvrir :
- Qu’est-ce qu’une projection cartographique ?
- Importance de définir un système de projection cartographique pour sa carte
- Quels sont les différents types de projection cartographique?
- Les systèmes de projections cartographiques le plus utilisés de nos jours sur le web
- Comment repérer les systèmes de projection d’une carte?
- Quel système de projection cartographique choisir pour votre carte?
Pensez à mettre cet article dans vos favoris, car la connaissance que vous allez y acquérir vous sera extrêmement utile.
Qu’est-ce qu’une projection cartographique ?

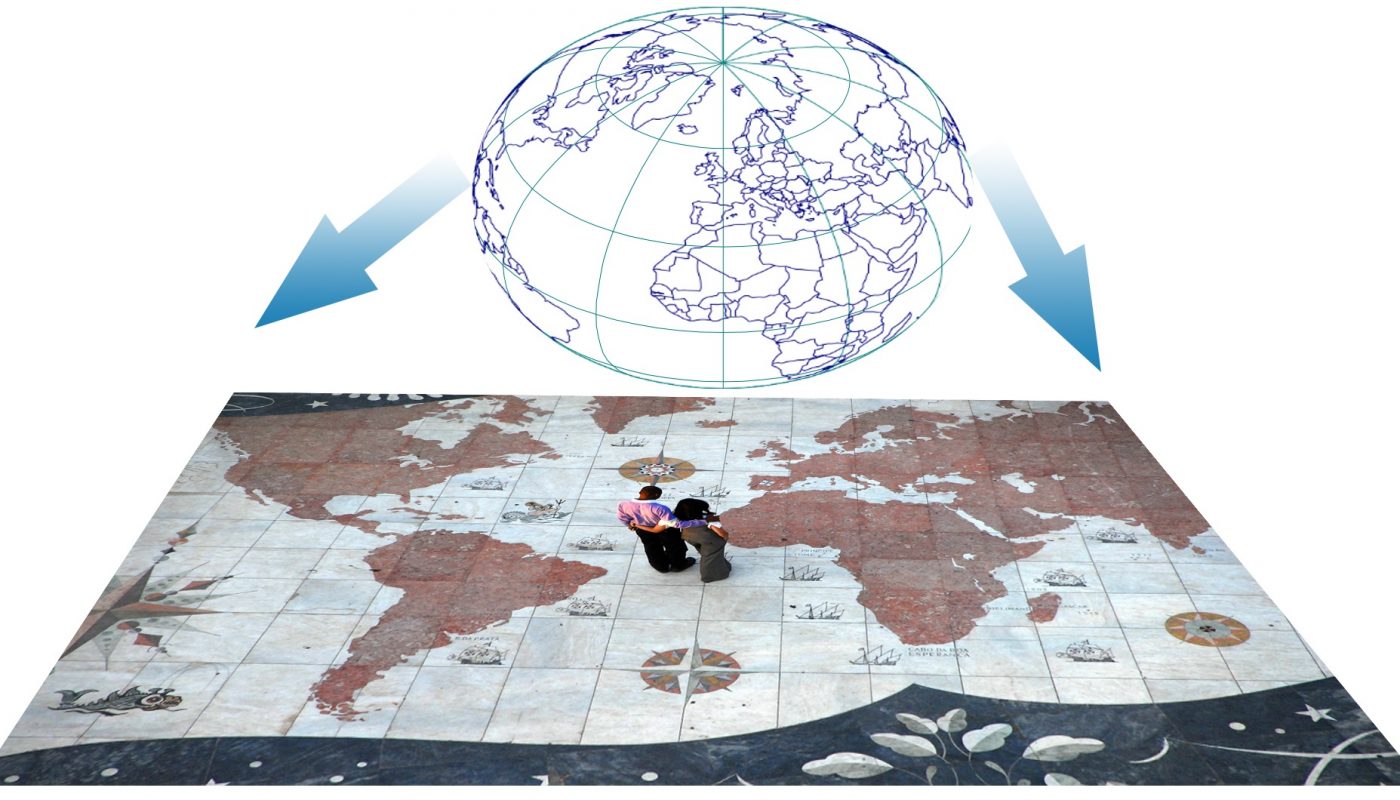
Comme vous le savez peut-être déjà, la terre est assimilée à une surface sphérique (une sphère). Pour faire nos études, nous ne pouvons pas nous référer à cette surface sphérique, car les dimensions réelles de la terre pourraient être difficilement observables à notre échelle de vision.
À défaut de faire les observations à travers les hélicoptères (pour avoir une vue en grand), nous nous devons de projeter nos détails de terrain sur un support qui nous sera facile à observer, une carte.
Le processus qui nous permet de représenter les objets situés sur la sphère terrestre (surface courbe) vers la carte (surface plane) est appelé projection cartographique.
Importance de définir un système de projection cartographique pour sa carte
Il y a un intérêt particulier à devoir définir un système de projection sur sa carte. Car l’un des objectifs pour lesquels les éléments sont représentés sur une carte, c’est pourqu’ils soient repérés.

Repérer un élément sur la carte, c’est reconnaitre ses coordonnées géographiques en l’occurrence la longitude, la latitude et l’altitude. Ces 3 éléments définissent ce qu’on appelle système de coordonnées cartographique.
Lorsque vous disposez de trois coordonnées géographiques d’un objet, vous pouvez le retrouver facilement sur le lieu physique (réel), il suffit de les enregistrer dans un GPS et de se laisser guider par celui-ci.
Définir le système de projection pour votre carte, c’est attribué aux objets représentés sur votre carte, leurs vraies coordonnées géographiques. Car lorsque vous créez une carte, le logiciel attribue par défaut des coordonnées fictives (undefinit system) ; il revient à vous de préciser ce système pour que les éléments de votre carte soient repérables.
Notation de coordonnées géographiques
Sur une carte, vous pouvez retrouver les coordonnées de longitude et latitude écrites de différente façon. Si vous n’êtes pas avisé, vous pouvez croire qu’il s’agit d’un tas de chiffres sans signification.
Au fait, cette différente manière d’écrire les coordonnées géographiques constitue différentes notations de coordonnées cartographiques.

Il existe principalement 2types de notation de coordonnées géographiques
- La notation angulaire
- La notation décimale ou UTM
Notation angulaire
C’est la notation qui associe les coordonnées au degré, minute et/ou seconde. Il en existe de 3types :
- DMS : degré-minute-seconde. Exemple : 49° 30′ 00″
- DM : degré-minute. Exemple : 49° 30,0′
- DD: degré décimal. Exemple : 49,500 0°
Dans un logiciel SIG, il existe des possibilités de transformer en un clic des milliers coordonnées de la notation DMS vers DD ou inversement.
Notation décimale (UTM)
Les coordonnées résultant de la projection UTM. Elles sont basées sur un système décimal. Ces coordonnées sont plus faciles à utiliser pour les calculs que les coordonnées angulaires géographiques.
La projection UTM découpe le globe en 60 fuseaux verticaux de 6° (tranche de méridiens espacés de 6°) et en 20 bandes parallèles. La France métropolitaine est située dans 3 fuseaux verticaux (30, 31 et 32) et dans 2 bandes parallèles (U et T).
Dans chaque fuseau, les coordonnées cartographiques sont données par les coordonnées :
- E, abscisse sur l’axe horizontale. Elle est mesurée en mètres d’W en E. Le méridien central du fuseau, à 3° du bord W et E, correspond à la valeur 500.. 000 m (500 km).
- N, ordonné sur l’axe vertical. Dans l’hémisphère N, elle est mesurée en mètres depuis l’équateur.
Exemple coordonnées UTM Refuge de Tête Rousse 32T 330 646 5 080 299
Dans un logiciel SIG, il possible de transformer en un clic des milliers coordonnés de la notation angulaire DMS ou DD vers la notation décimale ou UTM.
Types de projection cartographique
Il existe 3 catégories de projections par rapport à 3 considérations suivantes :
- Support de la projection,
- Conservation de propriétés,
- Position relative de la graticule, des pôles ou de l’équateur
Support de la projection
Par rapport au support utilisé pour la projection, on distingue 3types de projection :
- La projection conique : le support est un cône
- La projection cylindrique : le support est un cylindre
- La projection azimutale : le support est un plan horizontal tangent à la sphère terrestre.
Projection conique
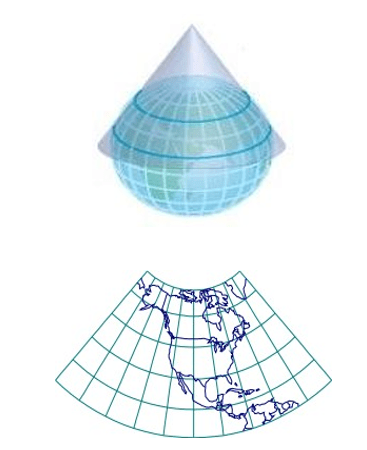
- Les projections coniques donnent l’apparence d’une surface conique développée qui pourrait être roulée en un cône.
- Ces projections sont des constructions mathématiques souvent plus complexes que la projection sur une simple surface conique.
- On peut y trouver une seule ligne, ou deux lignes, qui soient exemptes d’altérations de l’échelle.
Projection cylindrique
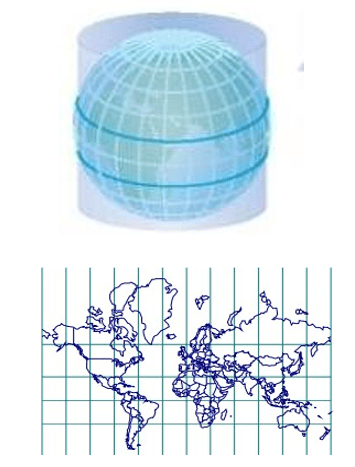
- Les projections cylindriques sont celles qui confèrent une apparence rectangulaire aux graticules.
- Le rectangle peut être vu comme le développement d’une surface cylindrique qui peut, à son tour, être enroulée en un cylindre.
- Les projections cylindriques sont souvent employées pour les cartes du monde
Projection azimutale
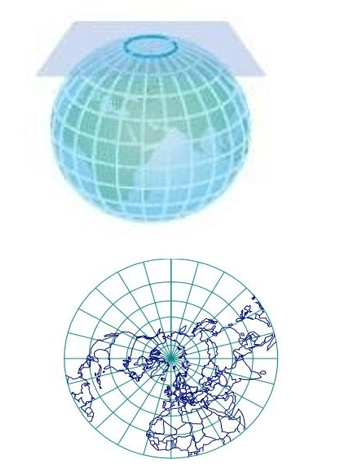
- Les projections azimutales sont celles qui préservent les azimuts (c.-à-d. les directions par rapport à une direction donnée, celle du nord dans leur aspect normal).
- Un point seul ou un cercle peuvent exister sans déformation d’échelle.
- Les exemples classiques de projections azimutales incluent la projection stéréographique et la projection azimutale équivalente de Lambert
Conservation de propriétés
Par rapport à la conservation de propriétés, on distingue :
- La projection équivalente qui conserve localement les surfaces ;
- La projection conforme qui conserve localement les angles, donc les formes ;
- La projection aphylactique qui ne conserve ni les surfaces, ni les angles, mais elle peut être équidistante, c’est-à-dire conserver les distances sur les méridiens.
Position relative de la graticule, des pôles ou de l’équateur
Par rapport à la position relative de la graticule, des pôles ou de l’équateur, on distingue :
- Projections polaires
- Projections normales
- Projections équatoriales
- Projections transverses
- Projections obliques
Projections polaires
- Une projection cartographique est dite polaire si l’image d’un pôle est au centre de la carte.
- L’aspect polaire est l’aspect normal des projections azimutales
Projections normales
- L’apparence et la position relative de la graticule, des pôles et de l’équateur sont les plus naturelles, au sens, le plus souvent, des principes de base de l’approche géométrique.
- L’aspect normal est celui qui découle de la forme la plus simple des calculs ou de l’apparence la plus simple du graticule.
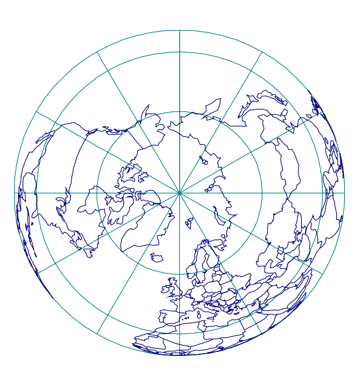
Projections équatoriales
- L’image de l’équateur est au centre de la carte.
- L’image de l’équateur est placée dans la direction de l’un des principaux axes de la carte, le plus souvent l’axe horizontal.
- L’aspect équatorial est l’aspect normal des projections cylindriques.
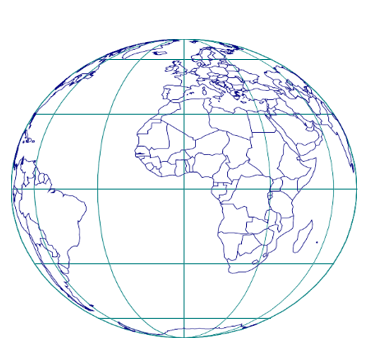
Projections transverses
L’apparence et la position relative de la graticule, des pôles ou de l’équateur dans la projection résultent de l’application des formules de la projection d’aspect normal à un globe préalablement tourné de 90° autour de son centre, de sorte que ses pôles se trouvent dans le plan équatorial original.
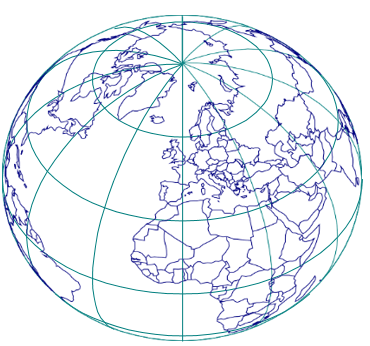
Projections obliques
Une projection cartographique n’est une projection oblique, où elle est sous un aspect oblique, si elle n’est ni polaire ni équatoriale, ni d’aspect transverse ou normal
Systèmes de projection cartographiques le plus utilisés de nos jours sur le web
Projection de Mercator transverse
La projection de Mercator transverse, également connue sous le nom de projection de Gauss-Krüger, est une projection où la ligne d’échelle constante est le long d’un méridien plutôt que sur l’équateur. Le méridien central et l’équateur sont des lignes droites.
Les autres méridiens et parallèles sont des courbes complexes dont la concavité est tournée vers le méridien central. La projection possède une échelle vraie le long du méridien central ou le long de deux lignes parallèles équidistantes du méridien central.
Elle est généralement utilisée pour des cartes à grande échelle, sur de petites zones. En raison de la distribution de la déformation, elle est habituellement utilisée en divisant la région à cartographier en zones de trois degrés (3°) ou de six degrés (6°) limitées par des méridiens.
Cette projection est très utilisée pour les cartes topographiques aux échelles comprises entre 1:25 000 et 1:250 000, et est à la base du système de coordonnées UTM.
Projection Lamber conique conforme
La projection conique conforme de Lambert, proposée par Johann Heinrich Lambert en 1772, montre les méridiens comme des droites régulièrement réparties convergeant en un des pôles.
Les angles entre les méridiens de la projection sont plus petits que les angles homologues sur le globe. Les parallèles sont des arcs de cercle qui sont tous centrés sur le pôle et dont l’espacement augmente au fur et à mesure qu’on s’éloigne du pôle. Le pôle le plus proche du parallèle standard est un point et l’autre pôle ne peut pas être représenté.
L’échelle est vraie le long du parallèle standard ou le long de deux parallèles standards, et elle est constante le long de n’importe quel parallèle donné. La projection conique conforme de Lambert est très largement employée pour la cartographie à grande échelle des régions dont la forme est allongée dans la direction est-ouest et pour les régions situées dans des latitudes moyennes. Elle est un standard dans beaucoup de pays pour les cartes à l’échelle de 1 : 500 000, aussi bien que pour les cartes aéronautiques aux échelles similaires.
Projection cylindrique équivalente de Lambert
La projection cylindrique équivalente fut proposée pour la première fois par Johann Heinrich Lambert en 1772. Elle est devenue la base pour beaucoup d’autres projections qui conservent de même les aires, telles la projection orthographique de Gall, ou les projections de Behrmann et de Trystan-Edwards.
Dans sa version originale, la projection de Lambert n’introduit qu’une seule ligne d’échelle constante, sur l’équateur. Les projections équivalentes qui s’en sont inspirées prennent deux parallèles comme lignes d’échelle constante.
Dans la projection cylindrique équivalente de Lambert, les méridiens apparaissent comme des droites parallèles équidistantes et la longueur de l’équateur vaut π fois celle des méridiens. Les lignes de latitude sont des droites parallèles dont l’espacement s’accroît en se rapprochant de l’équateur ; elles sont perpendiculaires aux méridiens. Changer l’espacement des parallèles est la méthode employée pour conserver les surfaces.
Les altérations des longueurs et des angles, cependant, deviennent très importantes dans les latitudes élevées à l’approche des pôles. Cette projection est rarement utilisée telle quelle pour faire des cartes, mais c’est un standard pour exposer les principes de la projection cartographique dans les manuels, et elle a grandement servi en tant que prototype à la conception d’autres projections.
Projection gnomonique
La projection gnomonique n’est ni conforme ni équivalente. C’est une projection en perspective azimutale où le point de projection est placé au centre de la Terre (d’où pour certains son nom : au centre de la Terre habitent les gnomes de la mythologie. Elle a été inventée par le grec Thalès, probablement aux alentours de 580 av. J-C. Tous les grands cercles du globe, dont tous les méridiens et l’équateur apparaissent comme des droites dans cette projection, une propriété qui lui est unique.
L’apparence de la graticule change avec l’aspect, comme c’est le cas pour les autres projections azimutales. Dans l’aspect polaire, les méridiens sont des droites qui s’intersectent au pôle central selon des angles qui sont les angles vrais. Les parallèles sont des cercles qui sont tous centrés sur le pôle ponctuel, et dont l’espacement augmente au fur et à mesure qu’on s’en éloigne. La projection ne peut montrer que moins d’un hémisphère. L’échelle augmente rapidement quand on s’éloigne du centre.
Ce qui la rend utile est sa qualité spécifique de représenter les grands cercles par des droites, ce qui aide les navigateurs et les aviateurs dans la détermination de la route la plus courte.
La projection Web Mercator
Nombreux sont les principaux services en ligne de cartographie à l’échelle urbaine [Bing Maps, OpenStreetMap, Google Maps, MapQuest, Yahoo Maps, et d’autres] à utiliser Web Mercator, variante de la projection de Mercator pour l’affichage cartographique. En dépit des évidentes déformations aux petites échelles, cette projection convient bien à une carte interactive mondiale dans laquelle zoomer sans raccords visibles jusqu’à obtenir des cartes à grande échelle, locales, où les déformations sont faibles du fait des qualités de quasi-conformité de la projection employée.
Le facteur d’échelle en un point donné d’une carte en projection conforme [telles la Mercator sphérique ou la Mercator ellipsoïdale] est uniforme dans toutes les directions à partir de ce point.
Pour la projection Web Mercator, le facteur d’échelle en un point varie ici dans toutes les directions. Il est en effet fonction des rayons de courbure du globe dans le plan méridien et dans le premier vertical du point, ainsi que de l’azimut de la direction.
Si on se contente d’utiliser Web Mercator pour imprimer la direction d’un nouveau restaurant à travers la ville, ou à des fins de visualisation sur l’écran de l’ordinateur ou pour d’autres utilisations sur le Web, il n’y aura aucun problème. Mais Web Mercator est une projection qui a étendu son domaine d’application [le Web] à un autre domaine [SIG], où elle démarre une nouvelle vie. En témoignent les codes EPSG, Esri et FME créés pour Web Mercator. Mais les géomètres et les professionnels des SIG se doivent de savoir que Web Mercator n’est pas une projection conforme. Si des calculs de distance sur une projection Web Mercator sont faits sans précautions [avec l’impression de la simplicité qui caractérise une projection conforme], ils seront erronés. Si on veut les effectuer correctement, ils demanderont beaucoup de travail.
Pour une région dont la taille est de l’ordre d’un quart d’hémisphère [l’Amérique du Nord par exemple], les différences paraissent légères. Il se trouve en effet que les valeurs en abscisses [easting] sont identiques. Les différences sont dans les ordonnées [northing]. Il n’y a aucune différence des ordonnées sur l’équateur, mais à la hauteur de 70 degrés nord, la différence est de 40 km. Cet étirement nord-sud de la projection Web Mercator est la raison de son caractère non conforme.
Les projections de Mercator sont utiles à la navigation parce que les loxodromies, ces lignes de cap vrai constant que les navigateurs utilisaient pour naviguer avant le GPS, y sont des droites. Mais, malgré son nom, nous devons garder à l’esprit que les lignes droites dans la projection de Web Mercator ne sont pas des loxodromies.
Pour résumer le cas de la projection Web Mercator :
- C’est une projection cylindrique
- Ses méridiens sont des droites équidistantes
- Ses parallèles sont des droites inégalement espacées, mais d’une manière qui n’est pas celle de la projection de Mercator conforme.
- Ses loxodromies ne sont pas des droites
- Ce n’est pas une perspective
- Ses pôles sont à l’infini
- Elle n’a pas été proposée par Mercator en 1569, mais par Google, récemment
- Elle n’est pas conforme
WGS 84 [World Geodetic System 1984]
WGS 84 est un système géodésique mondial. Il est composé d’un système de coordonnées, d’un ellipsoïde de référence, un géoïde. Ce système géodésique mondial est notamment utilisé par le système de positionnement par satellite GPS.
WGS84 est défini et maintenu par la Nationale Geospatial-Intelligence Agency [NGA] des États-Unis. Il est cohérent, à environ 1 cm près, avec le référentiel terrestre international [ITRF]. Il s’agit d’une donnée globale, ce qui signifie que les coordonnées changent dans le temps pour les objets fixés dans le sol.
Comment repérer les systèmes de projection d’une carte
Que ce soit sur une carte papier ou dans un logiciel SIG, il est possible de repérer le système de projection de la carte.
Sur une carte
L’éthique dans l’élaboration d’une carte exige aux créateurs de cartes de toujours ajouter le système de projection utilisé lors de l’élaboration de la dite carte. Ainsi si vous êtes en face d’une carte élaborée par un professionnel, vous devriez voir quelque part sur la carte soit au pied de la carte ou sur la partie latérale droite [ou gauche] ; l’indication du système utilisé.
Dans un logiciel SIG
Il est radicalement simple de repérer le système de projection d’une carte lorsque nous sommes sur un logiciel SIG. Car le pied de la plupart de logiciels de cartographie indique :
- les coordonnées géographiques du point sur lequel l’on se situe sur la carte
- l’échelle de la carte.
- Et aussi et surtout le système de projection de la carte.
Quel système de projection cartographique choisir pour votre carte ?
S’il existe tant de projections cartographiques, c’est parce qu’aucune n’est apte à satisfaire tous les besoins. Le choix d’une projection cartographique qui convienne à une application donnée dépend d’un ensemble de facteurs à savoir :
- l’objectif de la carte,
- le type de données à y faire figurer,
- la région du monde à représenter et l’échelle de la carte finale.
Dans les SIG, les jeux de données à grande échelle [couvrant une faible étendue géographique] sont généralement projetés à l’aide de projections conformes de manière à préserver les angles. Pour de telles applications, l’altération des aires est si faible au regard de l’étendue géographique qu’elle en est négligeable : une projection qui conserve les aires n’est donc pas nécessaire.
Généralement, les données à grande échelle sont destinées à des applications SIG dont l’étendue géographique est restreinte [par exemple, un bassin hydrologique, une région ou un État].
Les deux projections les plus communément utilisées pour ces échelles sont la projection conique conforme de Lambert et la projection de Mercator transverse, à la base du système UTM [Universal Transverse Mercator] et de la plupart des systèmes de coordonnées planes des États-Unis d’Amérique.
Pour les cartes mondiales à usage général, notre recommandation est d’éviter les projections cylindriques et de leur préférer certaines projections pseudo-cylindriques.